Hierarchical IP Core Generator for Quantum Fourier Transform Implementation in FPGA

Quantum computers consist of two parts - a classical computer and its quantum coprocessor or accelerator. The functioning of the main elements of a quantum coprocessor is described by a wave function. You can create digital elements in FPGAs, the operation of which will be described by the wave function, so called digital qubits. Due to the high computational complexity of quantum computing such as Shor’s algorithm of factorization, VHDL-descriptions of digital quantum units must be created for their implementation in FPGA. We offer a hierarchical generator of FPGA cores for quantum Fourier transform implementation which is part of Shor’s algorithm. The generator creates descriptions of both homogeneous and heterogeneous coprocessors. In addition, the generator creates test circuits to check the generated coprocessors. This makes it possible to study the created coprocessors, compare results of their functioning with ones of real quantum coprocessors and analyze them.

Shor’s algorithm

In Shor's algorithm, the problem of factorizing the number M is reduced to the problem of determining the period r of the function y = a^xmodM, which is calculated by the controlled units CU (Fig. 1), where a is an arbitrary integer. This is precisely the problem that a quantum computer solves. It is shown that the greatest common divisor GCD(a^r/2+1, M) can be a divisor of the number M. The subsequent finding of the greatest common divisor is performed by a classical computer.

If 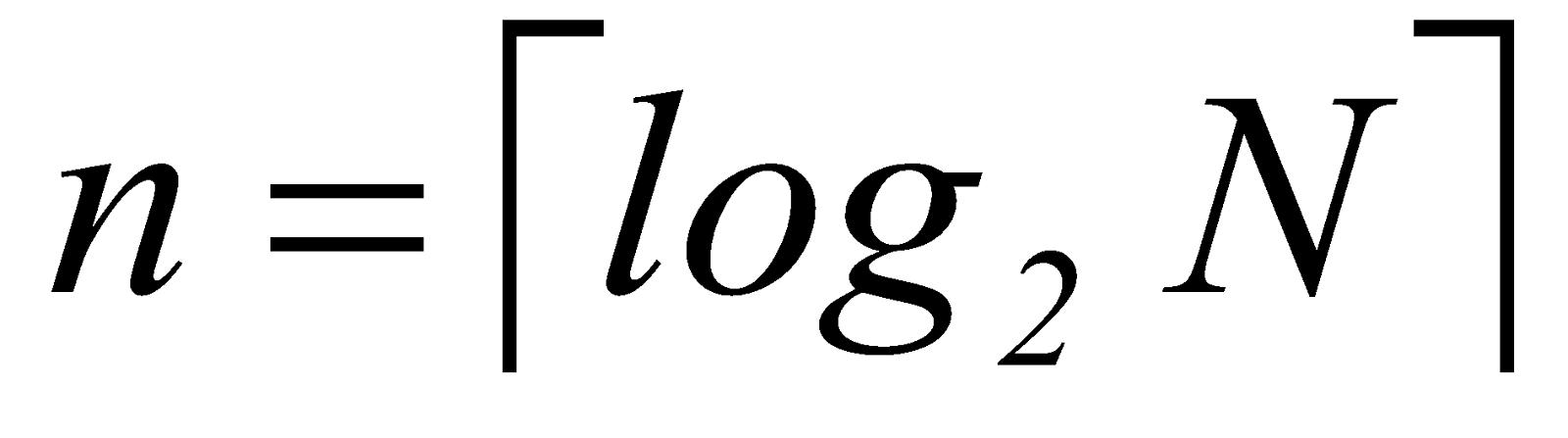 is the required number of bits to represent the number N to be factored than the upper quantum register in Fig. 1 requires at least 2n qubits, because Shor’s algorithm requires x to take values between 0 and at least N² and the modular exponentiation function can be written as .Shor's algorithm takes O(b³) time and O(b) space on b-bit number M inputs.

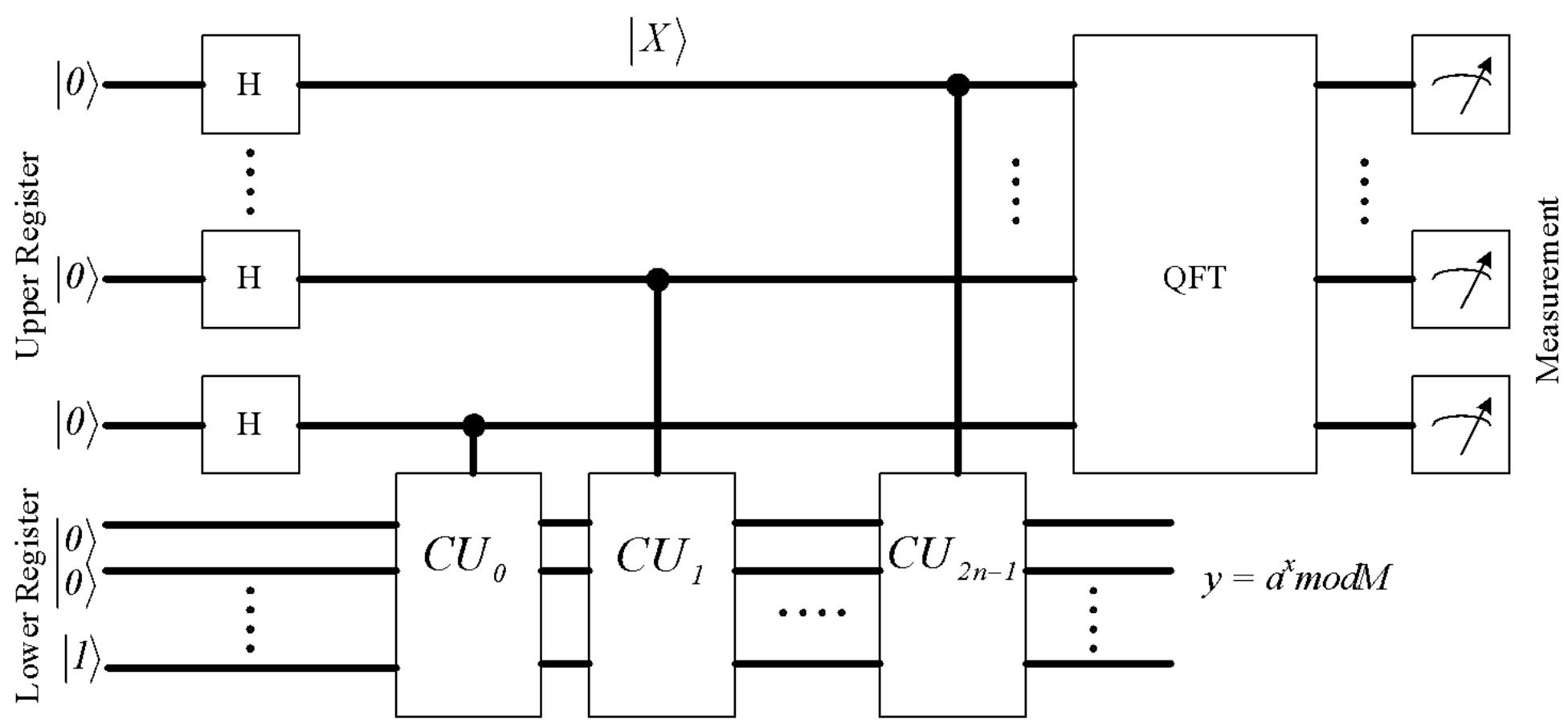
Fig. 1. Shor’s algorithm implementation

Each unit CUj calculates the value 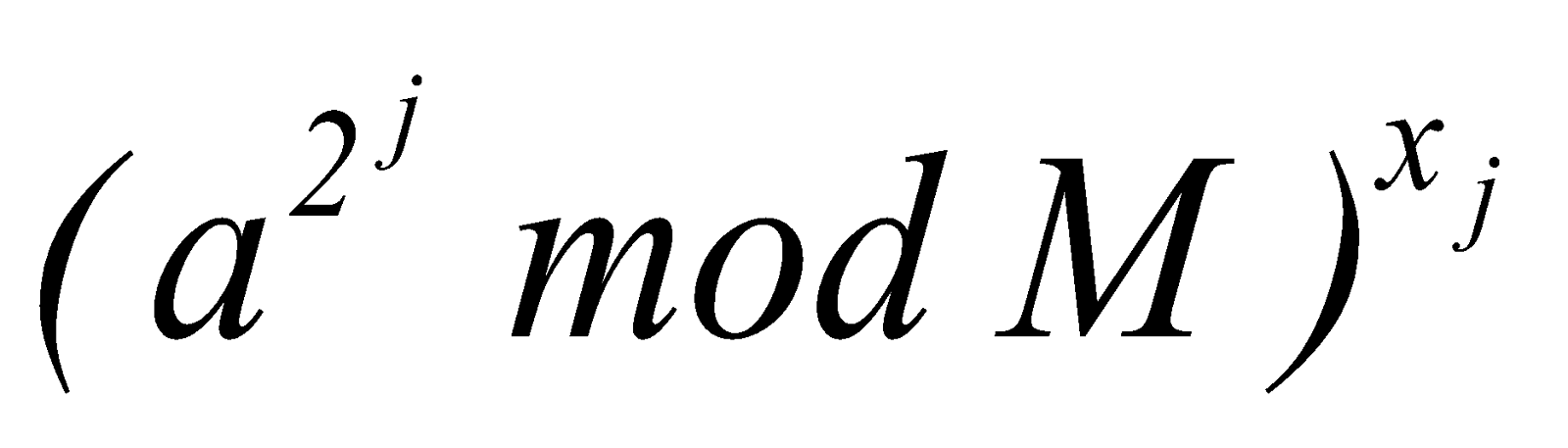, and unit CU_j^-1 finds the inverse function with respect to CUj.

QFT is used in calculations by the Shor algorithm. Its complexity is estimated as O(q), where q is the number of qubits. In addition, the QFT scheme (Fig. 2) uses only simple quantum gates, and there is no need to calculate inverse functions. This makes it easy to implement the QFT digitally using FPGA (Fig. 3).

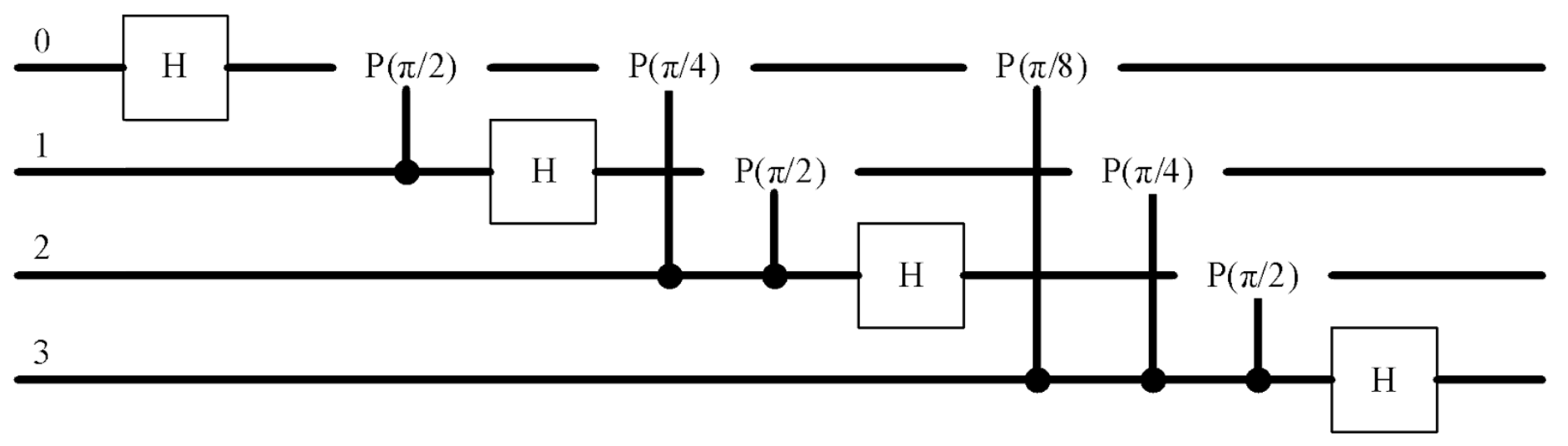
Fig. 2. Classical drawing of QFT (4-qubits)

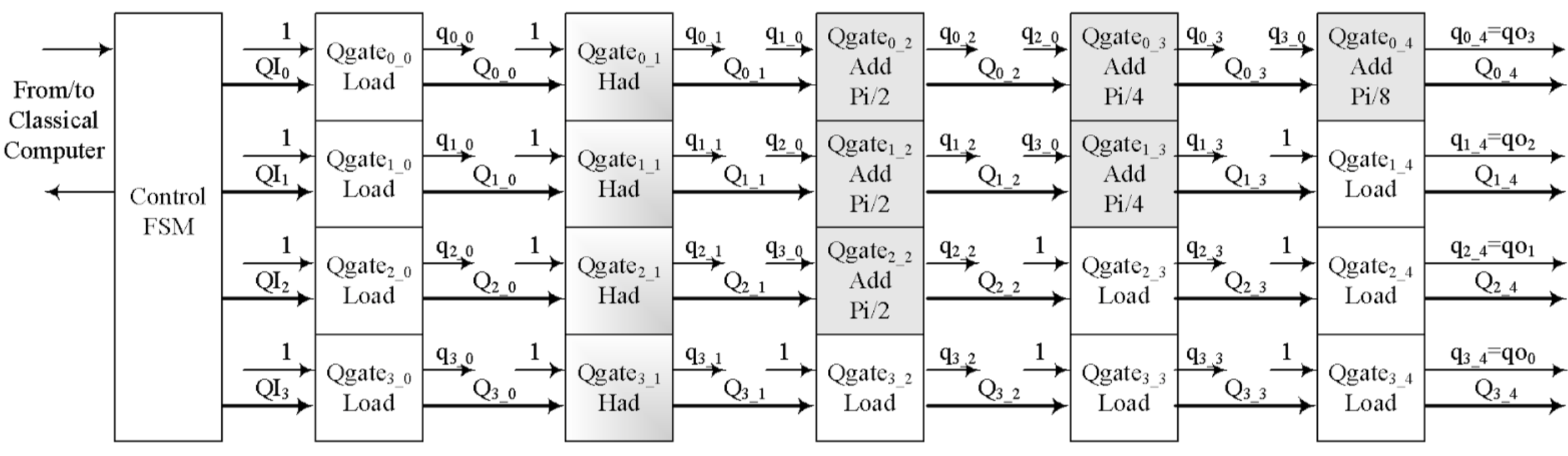
Fig. 3. Simplified drawing of QFT generated FPGA schema (4-qubits)

More difficulties arise when testing implemented on an FPGA circuit Fig. 3. So far, it has been possible to show its correct operation with a limited number of input vectors.

IP Core Generator hierarchy

The high computational complexity of quantum algorithms makes it necessary to create special core generators for FPGAs. 

First of all, a core generator for a quantum Fourier transform was created. The proposed core generator has a hierarchical structure.

The lowest level of the hierarchy is the level where digital quantum logic gates Fig. 4 are synthesized. The quantum logic gate includes an ALU, a comparator, and a pipelined register. ALU performs one of the conditional quantum operations. In this case, the code DataIn of the digital qubit previous state changes and turns into an output code DataO. The comparator compares this code with a random value Asin_f and forms the measured state of the qubit after performing the specified operation. The code of the new state of the qubit DataOut and its measured value 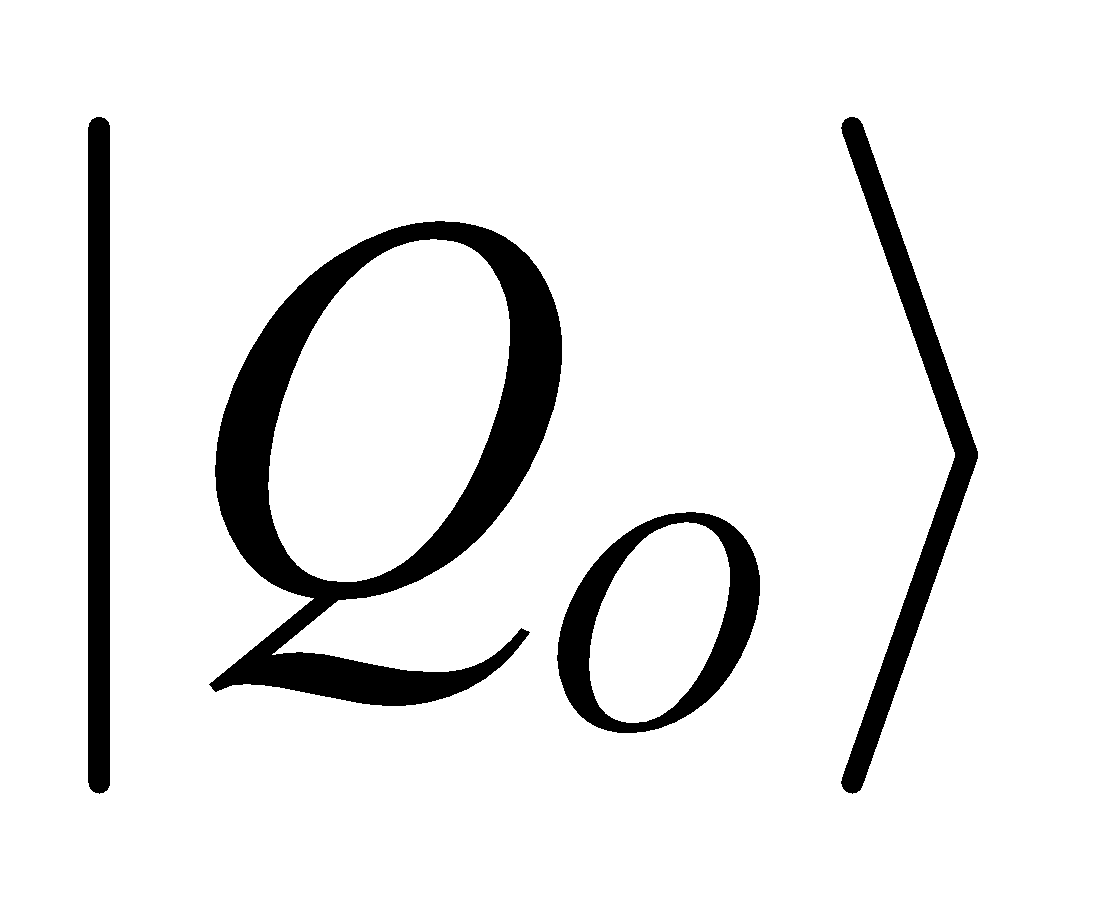 (after performing this operation) is issued from the output of the pipeline register RG.

In heterogeneous quantum coprocessors, each quantum gate receives its own random code for comparison. A schematic diagram of a digital quantum cell for this case is shown in Fig. 5. Near to the digital quantum gate is a pseudo-random number generator PRNG and a functional transformer 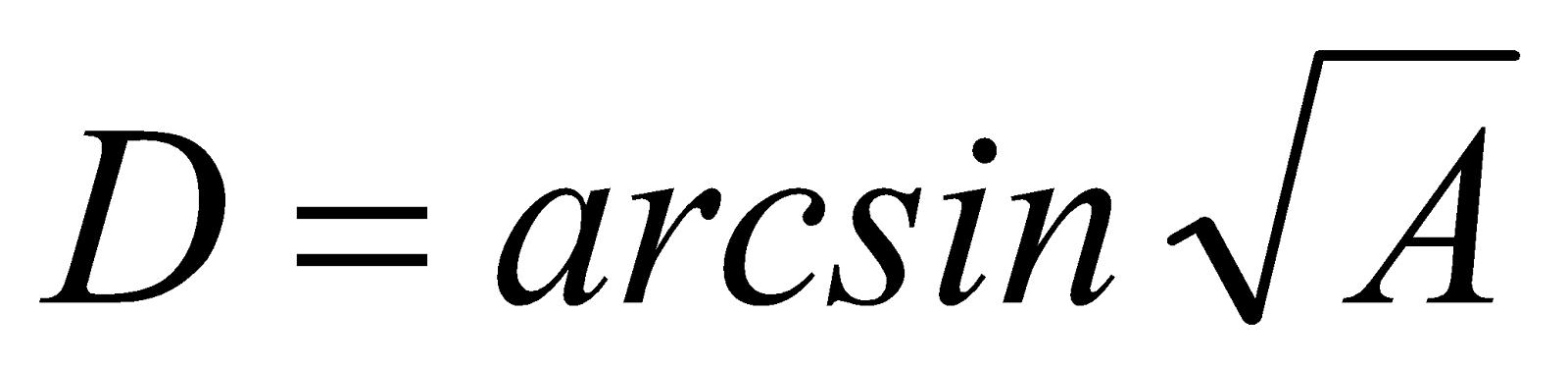. The level of digital quantum cells is the second level of the hierarchical core generator.

In this case, a digital qubit is formed by a serial connection of digital quantum cells (Fig. 6).

In homogeneous quantum coprocessors, all quantum gates receive the same random code for comparison. A schematic diagram of a digital quantum qubit for this case is shown in Fig. 7.

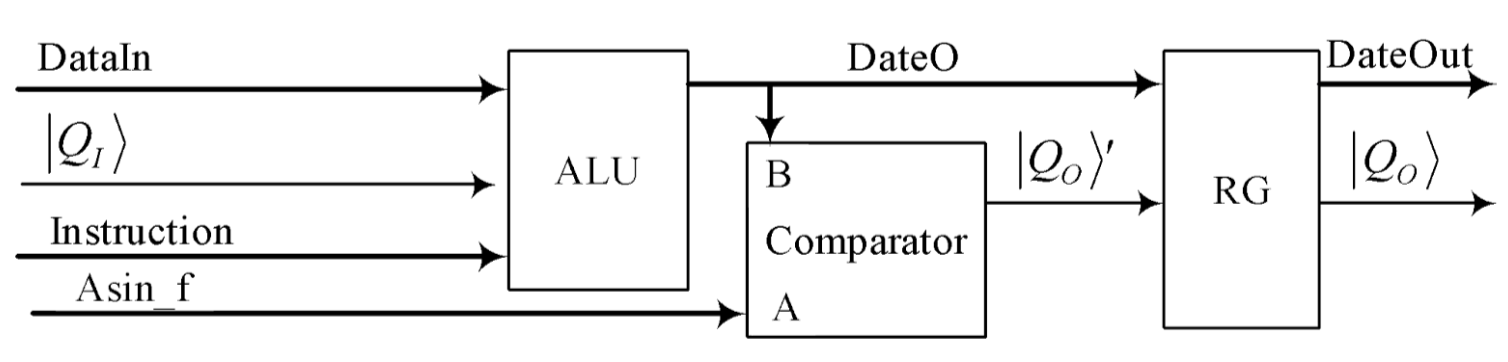
Fig. 4. A digital quantum gate Qgate

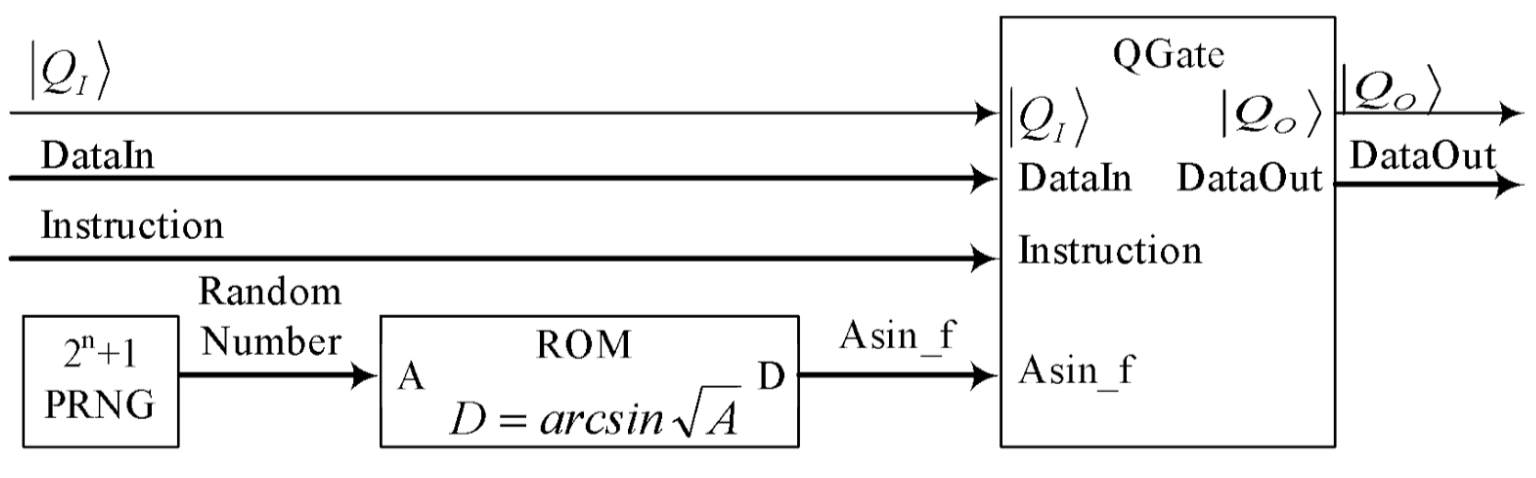
Fig. 5. A digital quantum cell DQCell for heterogonous digital quantum coprocessor.

The generalized scheme of a homogeneous digital quantum coprocessor is shown in the Fig. 9. There is only one pseudo-random number generator PRNG and one functional transforme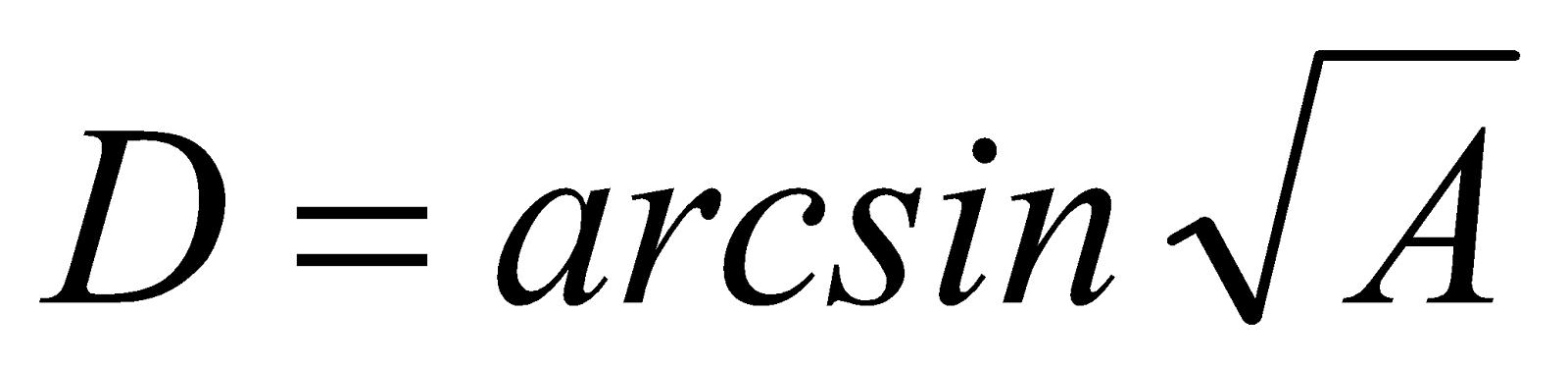r  in coprocessor. 

The digital qubit level is the third level of the hierarchical core generator.

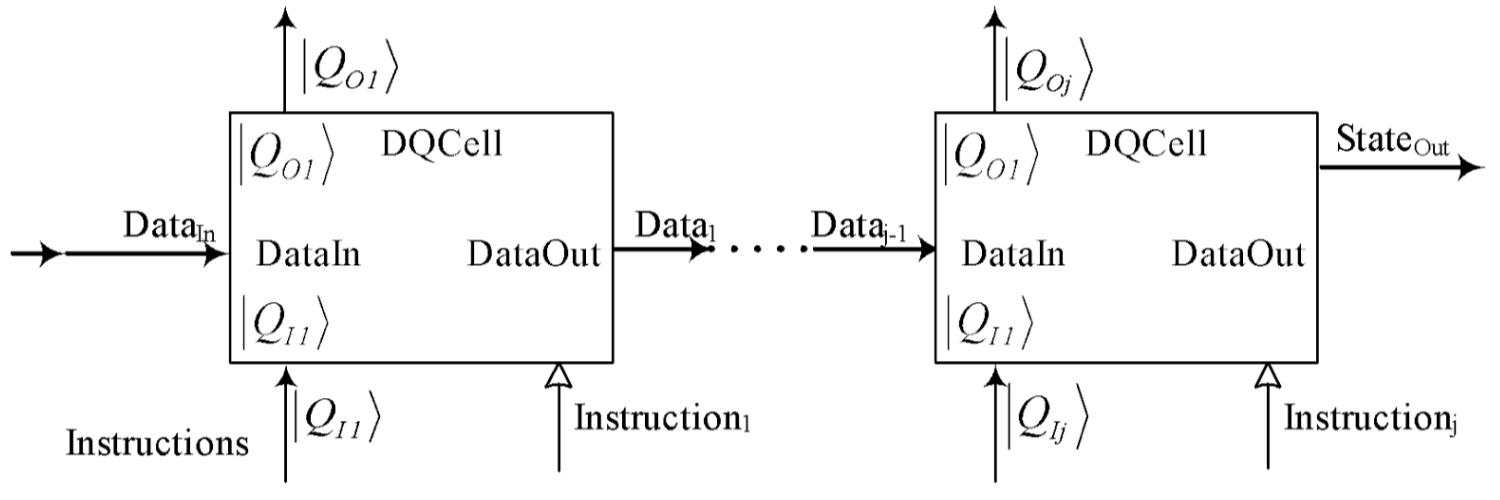
Fig. 6. A digital quantum qubit as line of DQCells for heterogonous digital quantum coprocessor.

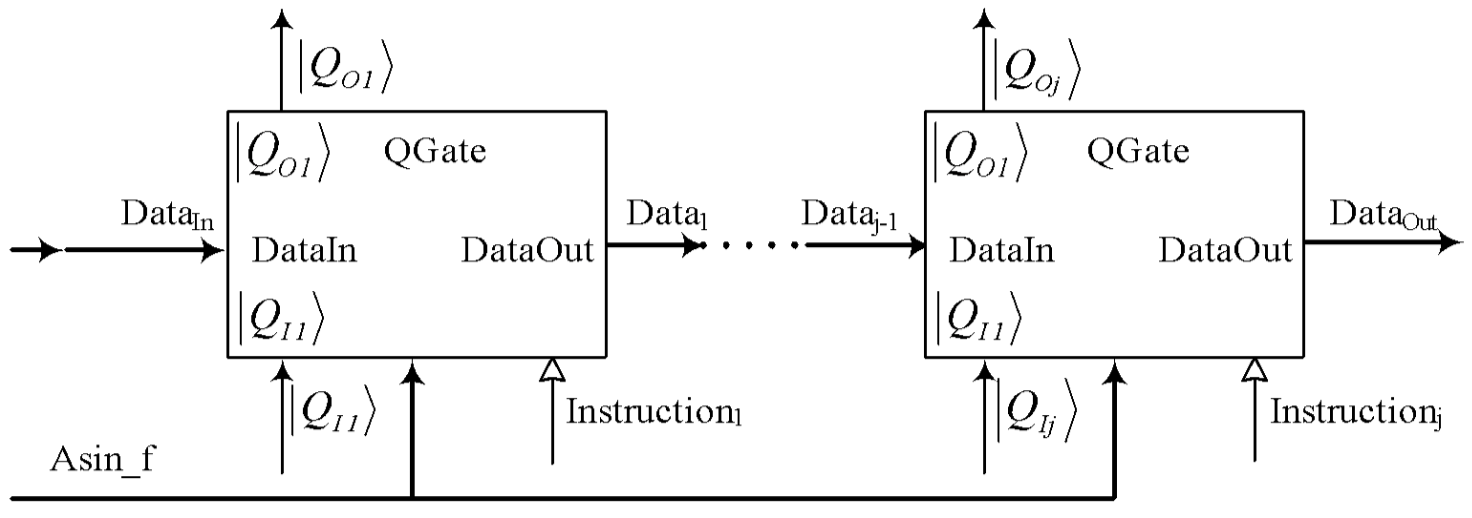
Fig. 7. A digital quantum qubit as line of DQGates for homogenous digital quantum coprocessor.

The classical scheme of the quantum Fourier transform is shown in Fig. 2. The same circuit based on the generated elements is shown in Fig. 3.

A testbench for simulating the operation (forth level) of the generated coprocessors is shown in Fig. 8. 

The testbench includes a Control Unit, an input register QiRgN, a coprocessor QFTN and a Test Unit for analyzing the results of the coprocessor operation (N is the number of qubits in the coprocessor, up to 1024). The test unit determines how often correct results appear on the coprocessor output. This is the fourth level of the hierarchy.

The fifth level of the hierarchy is the program of the control unit (in Fig. 8, N is digital qubits number) and global variables generation. And the highest level is the simulator.

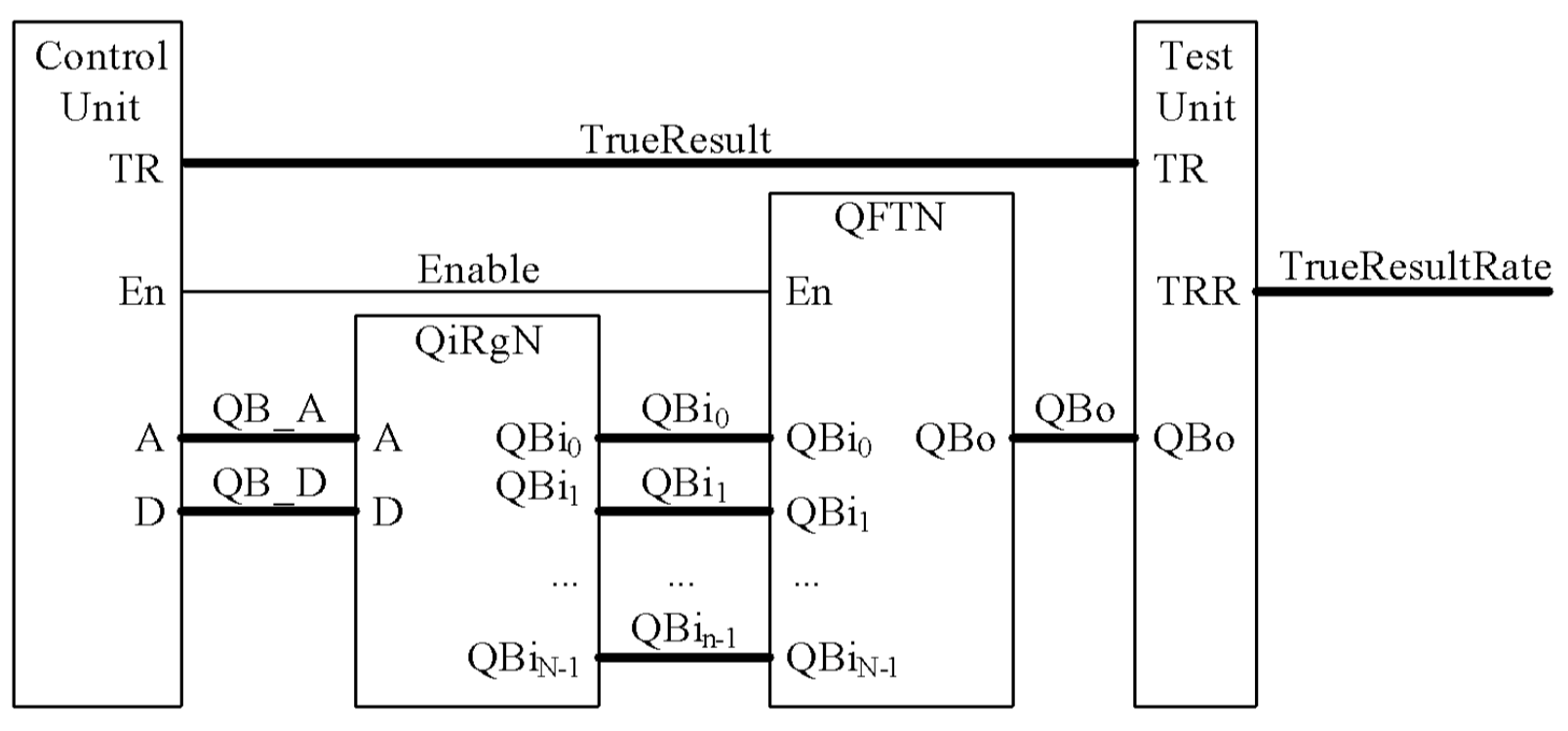
Fig. 8. Digital Quantum Coprocessor Testbench

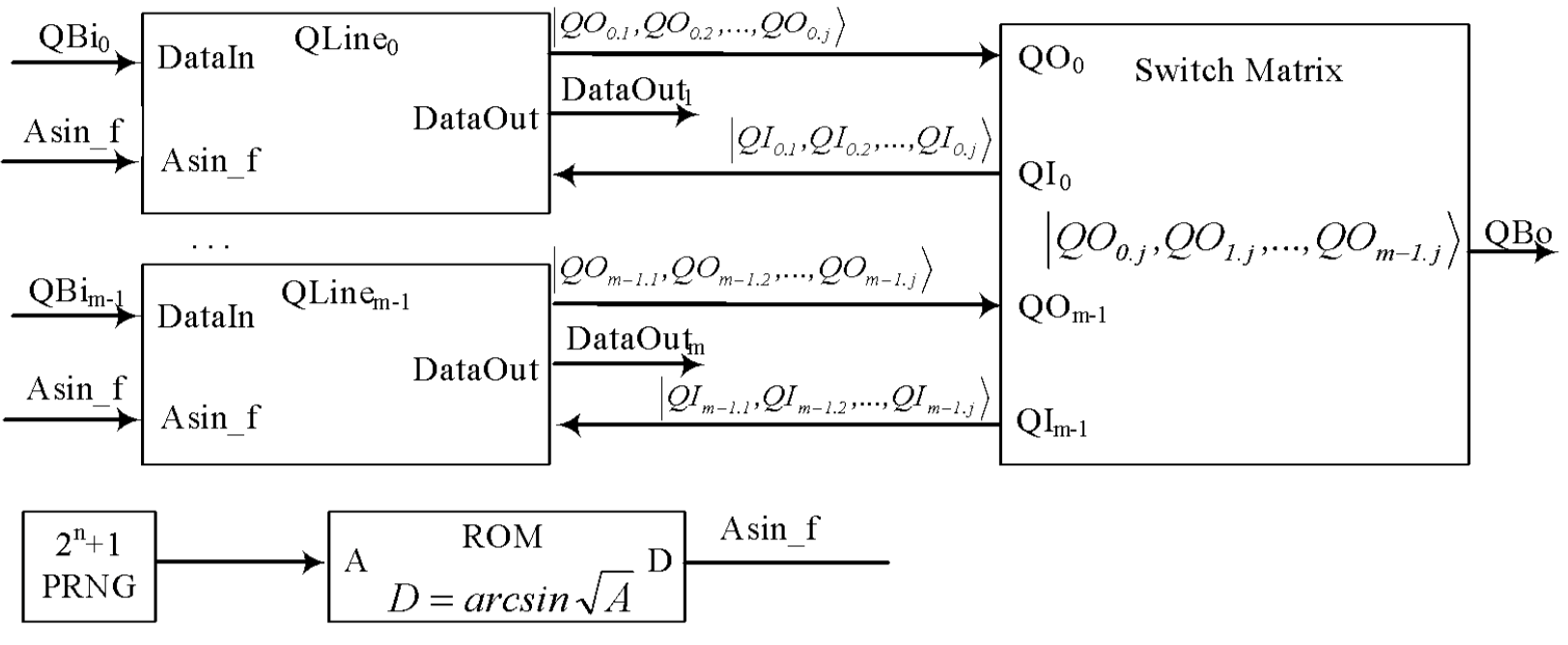
Fig. 9. A generalized functional diagram of a digital quantum coprocessor.